NEURON simulator¶
NEURON is a simulation environment to model neurons and networks thereof. NEURON itself is rather complex (neurons are complex things after all) and fairly low-level which results in lots of boiler plate code. There are some libraries(e.g. NetPyNE) that wrap NEURON and provide a higher-level interface to facilitate building models. In my experience these are typically geared towards creating models based on probabilities (e.g. “create 100 neurons with a 10% chance to be connected to another neuron”) rather than the well defined morphology/connectivity you get from e.g. connectomes.
navis does not try to emulate a full simulation suite but tries to fill a gap for people wanting to use non-probabalistic data (e.g. from connectomics) by providing an entry point for you to get started with some simple models and take it from there. At this point there are two types of models:
CompartmentModelfor modeling individual neuronsPointNetworkfor modeling networks from point
Compartment models¶
A CompartmentModel represents a single neuron (although you can connect multiple of these neurons) and is constructed from a skeleton (i.e. navis.TreeNeuron, see also navis.conversion.mesh2skeleton()).
import navis
import neuron
import navis.interfaces.neuron as nrn
# Load one of the example neurons (a Drosophila projection neuron from the hemibrain connectome)
# Note the conversion to microns!
n = navis.example_neurons(1).convert_units('um')
# Here we manually corrected the soma
n.soma = 20
# Reroot to the soma
n.reroot(n.soma, inplace=True)
# Create the compartment model
cmp = nrn.CompartmentModel(n, res=10)
NEURON compartment models are effectively collections of connected linear segments. Each of these segments can have its own set of properties and mechanisms. Here, we will use some biophysical properties from Tobin et al. (2017):
# Set the specific axial resistivity for the entire neuron in Ohm cm
cmp.Ra = 266.1
# Set the specific membran capacitance in mF / cm**2
cmp.cm = 0.8
# Add passive membran properties for the entire neuron
cmp.insert('pas',
g=1/20800, # specific leakage conductance = 1/Rm; Rm = specific membran resistance in Ohm cm**2
e=-60, # leakage reverse potential
)
At this point we already have a passive model of our Drosophila projection neuron. Next, we will determine what’s axon and what’s dendrite, and add a Hodgkins & Huxley mechanism so we have some actual action potentials to observe.
This will also illustrate one of the features of CompartmentModels: we keep a correspondence to the original skeleton via node (and connector) IDs. This allows you to modify, stimulate at or record from parts of the compartment model by using node IDs.
# Label axon/dendrite
navis.split_axon_dendrite(n, label_only=True, cellbodyfiber='soma')
n.nodes.head()
| node_id | label | x | y | z | radius | parent_id | type | compartment | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 0 | 126.272003 | 298.000000 | 224.496017 | 0.080000 | 2 | end | cellbodyfiber |
| 1 | 2 | 0 | 126.112007 | 297.840027 | 224.656006 | 0.146274 | 3 | slab | cellbodyfiber |
| 2 | 3 | 0 | 125.952003 | 297.520020 | 224.976013 | 0.277771 | 4 | slab | cellbodyfiber |
| 3 | 4 | 0 | 125.952003 | 297.200012 | 225.616013 | 0.277771 | 5 | slab | cellbodyfiber |
| 4 | 5 | 0 | 125.632004 | 297.040009 | 225.936005 | 0.277771 | 6 | slab | cellbodyfiber |
# A quick visualization
fig, ax = navis.plot2d(n, color_by='compartment', palette='tab10', lw=1.5)
# Label compartments
import seaborn as sns
for l in n.nodes.compartment.unique():
loc = n.nodes.loc[n.nodes.compartment == l, ['x', 'y', 'z']].values[-1]
ax.text(loc[0] + 10, loc[1], loc[2], l)
ax.elev = -110
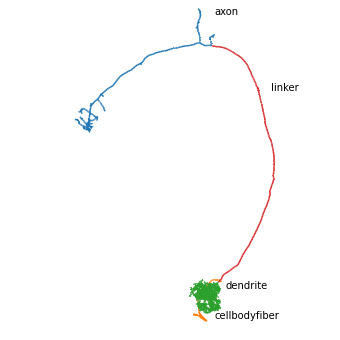
A little excursion about how NEURON represents neurons before we add the Hodgkins & Huxley (HH) mechanism: neurons consist of linear “sections” while individual (continuous) positions along each section are called “segments”. That distinction is important because our skeleton nodes correspond to segments but a mechanism such as HH is applied for entire sections.
# Collect axon nodes
axon_nodes = n.nodes.loc[n.nodes.compartment.isin(['axon', 'linker']), 'node_id'].values
# Get the sections for the given nodes
axon_secs = list(set(cmp.get_node_section(axon_nodes)))
# Insert HH mechanism at the given sections
cmp.insert('hh', subset=axon_secs)
Next we actually have to do something with our compartment model. For that we will add three voltage recorders: one at the soma, one at the base of the dendrites and one at the tip of the axon.
# Recordings and stimulations work via segments (as opposed to sections for mechanisms) -> hence we can use node IDs directly here
# Let's determine the tip of the axon and base of the dendrites programmatically using the
# geodesic distance
dists = navis.geodesic_matrix(n, from_=n.soma)
# Sort by distance from soma
dists = dists.iloc[0].sort_values()
dists.head(10)
20 0.000000
21 0.455753
19 0.633259
2409 0.836538
22 1.095767
18 1.113258
23 1.415775
2410 1.474030
24 1.692905
17 2.032377
Name: 20, dtype: float64
# Find the closest "dendrite" and the most distal "axon" node
dend = n.nodes[n.nodes.compartment == 'dendrite'].node_id.values
dend_base = dists.index[dists.index.isin(dend)][0]
print(f'Node at the base of the dendrites: {dend_base}')
axo = n.nodes[n.nodes.compartment == 'axon'].node_id.values
axo_tip = dists.index[dists.index.isin(axo)][-1]
print(f'Node at the tip of the axon: {axo_tip}')
Node at the base of the dendrites: 467
Node at the tip of the axon: 4384
# Add voltage recordings
cmp.add_voltage_record(dend_base, label='dendrite_base')
cmp.add_voltage_record(axo_tip, label='axon_tip')
cmp.add_voltage_record(n.soma, label='soma')
Last but not least we need to provide some input to our neuron otherwise it will just sit there doing nothing. We can add a current injection, trigger some synaptic currents or add a leak current. Let’s simulate some synaptic inputs:
# Get dendritic postsynapses
post = n.postsynapses[n.postsynapses.compartment == 'dendrite']
post.head()
| connector_id | node_id | type | x | y | z | roi | confidence | compartment | |
|---|---|---|---|---|---|---|---|---|---|
| 137 | 137 | 3736 | post | 135.232 | 291.104 | 210.840 | AL(R) | 0.906454 | dendrite |
| 138 | 138 | 635 | post | 132.872 | 284.448 | 196.056 | AL(R) | 0.928960 | dendrite |
| 139 | 139 | 4124 | post | 131.432 | 277.048 | 200.960 | AL(R) | 0.605084 | dendrite |
| 140 | 140 | 3176 | post | 124.984 | 286.568 | 216.480 | AL(R) | 0.922643 | dendrite |
| 219 | 219 | 3061 | post | 128.312 | 276.848 | 217.272 | AL(R) | 0.981077 | dendrite |
# Here we will open successively more synapses over 5 stimulations
for i in range(5):
# Onset for this stimulation
start = 50 + i * 200
# Number of synapses to activate
n_syn = i * 5
cmp.add_synaptic_current(where=post.node_id.unique()[0:n_syn],
start=start,
max_syn_cond=.1,
rev_pot=-10)
# Now we can run our simulation for 1000ms
# (this is equivalent to neuron.h.finitialize + neuron.h.continuerun)
cmp.run_simulation(1000, v_init=-60)
The compartment model has a quick & dirty way of plotting the results:
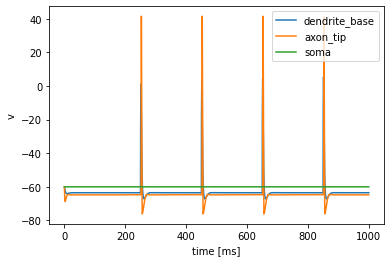
# Plot the results
axes = cmp.plot_results()
# Plot again and zoom in on one spike
axes = cmp.plot_results()
axes[0].set_xlim(240, 280)
(240.0, 280.0)
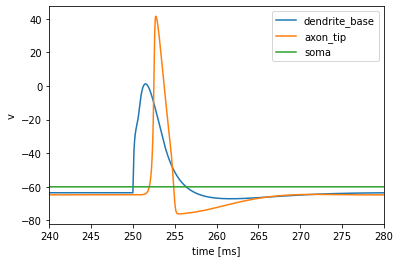
As you can see we get a nice depolarization at the base of the dendrites which elicits an action potential that we can measure in the tips of the axon. Because in our model the cell body fiber (i.e. the neurite that connects the soma to the base of the dendrites) is passive, the depolarization of a single spike attenuates before it reaches the soma.
Alternatively, you can access the recorded values directly like so:
cmp.records
{'v': {'dendrite_base': Vector[0], 'axon_tip': Vector[1], 'soma': Vector[2]}}
cmp.records['v']['dendrite_base'].as_numpy()
array([-60. , -60.04157854, -60.07494932, ..., -63.52188478,
-63.52188478, -63.52188478])
Next, let’s try to simulate some noisy input where the presynaptic neuron spikes multiple times:
# First we need to reset our model (by re-assigning `cmp` the old model will be garbage-collected)
cmp = nrn.CompartmentModel(n, res=10)
# Set properties and mechanisms
cmp.Ra, cmp.cm = 266.1, 0.8
cmp.insert('pas', g=1/20800, e=-60)
axon_secs = list(set(cmp.get_node_section(axon_nodes)))
cmp.insert('hh', subset=axon_secs)
# Add recording
cmp.add_voltage_record(dend_base, label='dendrite_base')
cmp.add_voltage_record(axo_tip, label='axon_tip')
cmp.add_voltage_record(n.soma, label='soma')
# Also add a spike counter at the axon
cmp.add_spike_detector(axo_tip, label='axon_tip')
# Now add a noisy preinput to say 20 dendritic postsynapses
post = n.connectors[(n.connectors.compartment == 'dendrite') & (n.connectors.type == 'post')]
cmp.add_synaptic_input(post.node_id.unique()[0:20],
spike_no=20, # produce 20 presynaptic spikes
spike_int=50, # with an average interval of 50ms: 20 * 50ms = over 1s
spike_noise=1, # very noisy!
cn_weight=0.04)
# Run for 1s
cmp.run_simulation(1000, v_init=-60)
# Plot results
axes = cmp.plot_results()
axes[1].set_ylabel('spikes [Hz]')
Text(0, 0.5, 'spikes [Hz]')
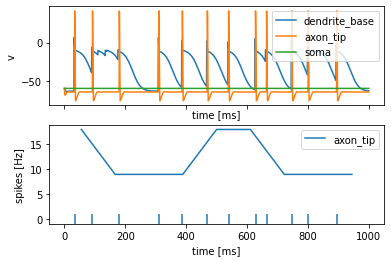
Note how we still don’t see a depolarization in the soma? While that might be a genuine biological feature of this neuron, I suspect there is something wrong with the radii along the cell body fiber - perhaps a pinch point somewhere? This just illustrates that good skeletons are paramount and you should critically inspect the results of your models.
Many methods in CompartmentModel try to use sensible defaults to make sure that you get some sort of effect. That said, it’s advisable that you adjust parameters as you fit your model to real world data. Check the help to see what you can do:
# Try this for example
cmp.add_synaptic_input?
Networks¶
While you can link together multiple compartment models to simulate networks this quickly becomes prohibitively slow so run. For larger networks it can be sufficient to model each neuron as a single “point process”. PointNetwork lets you quickly create such a network from an edge list.
In this tutorial we will use toy data but it is just as straight forward to plugin real data:
# First create a small 3 way network where one of the neurons (B) is inhibitory
import pandas as pd
edges = pd.DataFrame([])
edges['source'] = ['A', 'B']
edges['target'] = ['C', 'C']
edges['weight'] = [0.5, -1]
edges
| source | target | weight | |
|---|---|---|---|
| 0 | A | C | 0.5 |
| 1 | B | C | -1.0 |
# Next initialize network from edge list
net = nrn.PointNetwork.from_edge_list(edges, model='IntFire4')
net
PointNetwork<neurons=3,edges=2>
So far, our network won’t do anything because it doesn’t have any input. Let’s add an input to neurons A and B, and try that out:
# Add the stimulus
net.add_stimulus('A', start=100, stop=1000, frequency=100, randomness=0)
net.add_stimulus('B', start=600, stop=800, frequency=100, randomness=0)
# Run simulation
net.run_simulation(1000)
# Plot
ax = net.plot_raster(backend='matplotlib', label=True)
ax.set_xlim(0, 1000)
(0.0, 1000.0)
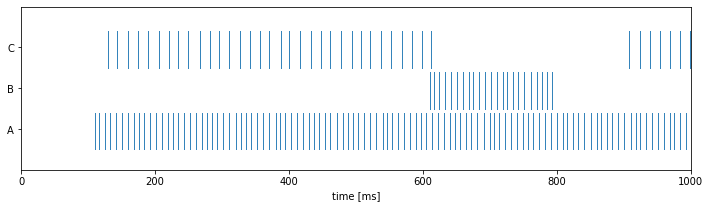
This toy example worked quite well: spikes in neuron A elicit occasional spikes in C via temporal summation. Activity in the inhibitiory neuron B hyperpolarizes C and it stops firing until well after activity in B has ceased.
The NEURON interface is a very recent addition and it might well change in the future (or become its own package). Functionality is also still limited and while I don’t intend to write a feature-complete wrapper for NEURON, I do welcome feature requests or contributions on Github.